RETURN to the CHEM 498C Home Page

DC and AC Circuits and Measurements

Chemistry 498A/C Laboratory, Fall 1997

Equipment required: Heath Voltage Reference Source (VRS) , resistance decade box, variable power supply, precision 10-turn Helipot with turns counting dial, 100 µA panel meter, resistance substitution box, digital multimeter, Hitachi Model V-355 dual-trace 35 MHz oscilloscope, EICO sine-square wave signal generator.

A: Basic DC Measurements

1. Familiarize yourself with the controls and connections on the Heath Voltage Reference Source (VRS) and the digital multimeter. Put the multimeter on its DC voltage ranges and measure a couple of voltages from the VRS to verify their proper operation and calibration. The VRS and the digital multimeter should agree within about 1%.

2. Internal resistance of a moving-coil panel meter

Moving-coil panel meters are usually labeled with their full-scale currents, but not usually with their internal resistances. However, you need to know this in order to calculate the values of series resistors for passive voltmeter (and shunt resistances for passive ammeters). It is best not to try to measure the internal resistance by means of the ohmmeter function of your digital multimeter, because some ohmmeters may generate enough current to damage sensitive meters. There is a safe way, however, utilizing Ohm's Law.

Set the resistance substitution box to 220 KOhms (high range) and connect it in series with the 100µ A panel meter and the output of your variable power supply.

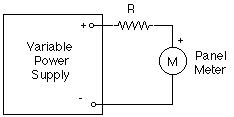
Turn on the power supply, turn up the voltage until the panel meter reads full-scale. Now use your digital multimeter to measure the voltage across the panel meter terminals, and, given that the full-scale current on the meter is 100µ A, calculate the internal resistance by Ohm's Law.

Measured full-scale voltage across panel meter ___________

Calculated internal resistance of panel meter _____________

3. Passive voltmeter

Calculate the series resistance needed to make a 10 volt full-scale passive voltmeter from your 100µ A panel meter. Given that we have plenty of 100 KOhms 1% precision resistors on hand, calculate the simplest way you could make the required series resistance by series and/or parallel combinations of larger or smaller resistance values. We have a large collection of 10% carbon resistors in all the "standard" values, stored in the small parts cabinets on the side of the laboratory. Look at these standard resistance values and choose the closest standard values(s) that will give you a total resistance in your series/parallel combination that is within 0.5% of the theoretically required value. Sketch the circuit of your passive voltmeter and label the standard resistance values that you intend to use.
Estimate the expected accuracy of your resistance combination, given the accuracy of its components.

Estimated accuracy, percent relative ______________

In this application, do you have to be concerned about the power rating of your resistors? Why or why not? _______________________________________________________

______________________________________________________________________

4. Output voltage and resistance of mystery voltage source.

You will be given a box with two terminals. This is the Mystery Voltage Source. Your tasks are (a) to measure the open circuit voltage across the terminals, in the most accurate way you can think of, using any equipment present in the laboratory, and (b) to estimate the output resistance of this voltage source. Hint #1: if the output resistance of this device is very large, then you won't know how accurately the digital multimeter can measure it, considering the likelihood of loading errors and given that you don't know exactly what the digital multimeters input resistance is on its DC voltage ranges. Hint #2: Here is one way to measure output resistance. Vb represents the ideal open-circuit voltage and Rout its output resistance. Connect a variable resistance R cross the output and vary it until the measured output voltage drops to one-half. Then R = Rout.

Describe below how you measured the output voltage of your Mystery Voltage Source.
Number of your box __________________
Open circuit output voltage ___________________
Output resistance ____________________

B. Oscilloscope and signal generator operation

1. Turn on the oscilloscope and the sine-square wave signal generator.

2. Set the sine-square wave signal generator to 60 Hz and turn the sine output level control all the way up (fully clockwise).

3. Set the following initial conditions on the oscilloscope:

4. Connect the sine wave generator output to the Channel 1 vertical input of the oscilloscope. Adjust channel 1's vertical position vertical position control until the waveform is centered. Adjust the brightness and focus controls (just to the right of the screen) to obtain a clear display. You should see a little more than one complete cycle of a sine wave.

5. Adjust the trigger level control slightly and notice the effect on the displayed waveform. The trigger level control determines the vertical deflection (voltage) at which the horizontal sweep is triggered. What happens when the trigger level is set higher (or lower) than the waveform goes? Try it. The same thing happens if the peak signal level is so low that it never exceeds the trigger level setting. Now set the trigger mode to AUTO and try it again. When the trigger mode is set to NORM, the trace simply disappears when triggering fails to occur. When the trigger mode is set to AUTO, then even if the signal never exceeds the trigger level, the horizontal sweep is triggered automatically at some arbitrary minimum rate. This way you will always have a trace, even when the input signal is zero or very low. Leave the trigger mode to AUTO. Pull out the trigger level knob to set the trigger slope of negative and note the effect. This control determines whether the trigger will be generated on the up-slope (+) or the down-slope (-). Push the trigger level knob back in. Switch the trigger source switch to LINE. The sweep is now triggered by the 60 Hz power frequency rather than by the displayed signal. Why does the waveform seem to drift across the screen? Switch the trigger source switch back to INT. Make sure you understand the relationships between these controls and the displayed waveform.

6. Measure the maximum peak voltage Ep and frequency (which is the reciprocal of the period) of the signal generator sinewave output.

Peak voltage: ______________volts. (Should be about 10 volts)

Frequency: _______________ Hz.

7. Measure the signal generator's sinewave output voltage using a digital voltmeter set to the AC voltage ranges. Compare this reading to the peak voltage measured by the oscilloscope and show how these two readings are supposed to be related to each other theoretically.

Meter reading ____________ volts

8. Connect the square-wave output of the signal generator to the oscilloscope's channel 2 input. Set the display MODE dial to CHOP and the INT TRIG switch to CH 1. Note that you can adjust the vertical position of the two waveforms independently with the two vertical position controls, but that they share a common time axis.

C. RC filters

1. A low-pass filter is supposed to pass low-frequencies with little attenuation and to attenuate (reduce) high frequencies. The simplest type of filter is the RC filter. Construct an RC low-pass filter from a 10K resistor and a 0.02 µf capacitor (these values need only be approximate).
input 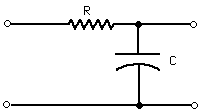output
Connect the sine output of the signal generator to the input of the filter and observe this signal on channel 1 and the output of the filter on channel 2 of the oscilloscope. Set the display MODE dial to CHOP and the INT TRIG switch to CH 1. Adjust the vertical position controls for the two channels so that zero is in the center of the screen for both signals.

2. Measure the peak amplitude Ep of the input and output signals for frequencies of 20 Hz, 50 Hz, 100 Hz, 200 Hz, and so on up to as high as you can go. Plot the ratio of output to input voltage vs frequency on log-log paper. At which frequency is the output/input ratio equal to 0.707 ? This is called the corner or roll-off frequency.

Measured corner frequency ____________ Hz.

Compare this to the theoretical value of 1/2[pi] RC. _____________ Hz

What phase shift did you observe between input and output signals at low frequencies? ____________ At high frequencies? __________

RETURN to the CHEM 498C Home Page